Geomechanics of Compressibility – Part I: Why Is It Important?
- PetroGem Inc.

- Jan 26, 2016
- 4 min read
After encountering frequent misunderstandings of rock compressibility and its applications, I decided to write a series of posts on ‘geomechanics of compressibility’ to explain its rock mechanical definition, its different types, methods of compressibility measurement and their differences and the parameters affecting this property especially stress path and hysteresis. As an introductory post, let’s start with explaining why compressibility is important to us. But wait a moment! If you feel the equations are eyesores just ignore them, I don’t think it will really matter.
Fluid Flow Analysis
Pore volume compressibility (Cp) has long been recognized as an important factor in fluid flow simulation for aquifers and reservoirs as shown by the following fundamental equation of fluid flow in porous media:
(Cp+Cl)ρφ ∂p/∂t+∇.(-k/μ(∇p+ρg∇z)=q [In this equation, Cl is fluid compressibility, ρ is pore fluid density, φ is rock porosity, g is gravity acceleration, q is the source term, k is permeability, t is time and z is the elevation measured in the vertical direction oriented downward.]

Figure 1. An old but popular graph based on laboratory tests used for estimation of rock compressibility for fluid flow analysis in reservoirs. (source: Hall, 1953).
Generally, in either of fluid flow simulations or material-balance calculations, the role of pore volume compressibility coefficient (Cp) becomes increasingly important as the fluid compressibility decreases. The importance of pore volume compressibility is even more crucial for closed systems where, in absence of fluid flux, fluid flow and pressure changes are controlled mainly by pore volume changes.
Hydrocarbon Reserve Estimation and Storage Capacity Evaluation
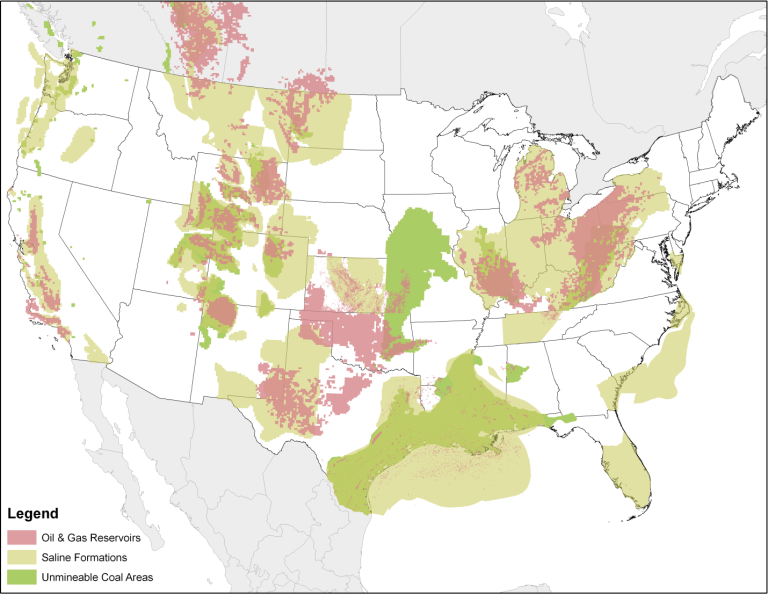
Figure 2. Assessment of potential CO2 storage in United States (Source: www.epa.gov)
Pore volume compressibility is also important in volumetric estimation of hydrocarbon reserves(find more in here) and evaluation of fluid storage capacity and efficiency in aquifers (for instance, waste fluid disposal or CO2 sequestration). As a simple example, in estimation of storage capacity of closed-system aquifers, the efficiency factor (Ei) for storage is introduced by Zhou et al. (2008) as:
Ei=(Cp+Cw )Δp[where Cw is the compressibility of water and Δp is the average pressure increase within the aquifer induced by injection.]
Approximation of Porosity Variation
Another application of pore volume compressibility is for the estimation of porosity change induced by pore pressure variation within a reservoir. The following equation is widely used for porosity approximation of consolidated and cemented reservoir rocks (e.g., Satter et al., 2008):
φ2=φ1 exp(Cp(p2-p1))[where φ1 and φ2 are the values of porosity, at reservoir pressures of p1 and p2, respectively.]
Such relations are the most simplistic way of involving geomechanics in fluid flow simulation. However, as it can bee seen in Figure 3, such relations must be used with the most caution as I will discuss it in detail later in this series.

Figure 3. Variation of porosity with two consecutive cycles of pore pressure change (injection/production) in a uniaxial pore volume compressibility test (UPVT) for a sample from a sandstone formation in Alberta, Canada (Source: Soltanzadeh, 2016).
Estimation of Ground Deformation
Bulk volume compressibility coefficient, when measured using a uniaxial pore volume test, can be directly used for calculation of reservoir or aquifer contraction or expansion induced by production or injection.
In general, the expansion of ΔH induced by the average pore pressure increase of Δp in a reservoir or an aquifer with an average height (thickness) of H may be calculated from the following equation:
ΔH= CbuΔpH[where Cbu is uniaxial compressibility.]
Some rocks, such as consolidated sandstones, behave elastically when stresses are less than critical yield stresses. Rocks show more elastic responses when pore pressure is increased e.g., in the case of waste fluid disposal or CO2 sequestration (Fjær et al., 2008). When rock behaviour is isotropic and elastic, the following relation exists between uniaxial bulk compressibility and rock elastic parameters:
Cbu=((1-2υ)(1+υ))/(E(1-υ))[where υ is Poisson’s ratio and E is Young’s modulus of the rock.]
Hence, in absence of other reliable data, bulk volume compressibility can be used as an auxiliary parameter for estimating elastic properties of the rock.

Figure 4. Historic 1977 photo depicting the location of maximum land subsidence in the U.S., near Mendota, CA in the San Joaquin Valley. Joseph Poland (pictured), USGS, scientific subsidence studies pioneer, placed the date signs to indicate previous elevations (Source: www.voanews.com).
Calculation of Biot’s Coefficient
Bulk volume compressibility coefficient (Cb) may also be implemented in the following equation to estimate Biot’s coefficient (α) as a key parameter required for any geomechanical analysis:
α=1-Cm/Cbwhere Cm is the matrix (or grain) compressibility and can be measured using an unjacketed hydrostatic test, or it can be estimated from the mineralogical composition of the rock (Zimmerman,1991).

Figure 5. Maurice Anthony Biot (1905-1985) in his apartment at 300 Central Park West, New York, September 1964 (Source: www.olemiss.edu)
Read the second part of this series here.
References











Comments